
A radical expression is composed of 3 main parts.
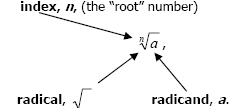
1. radicand
- the number whose nth root you should get
- recall, the radicand is the entire expression under the radical, even if it’s composed of several terms or factors.
2. the radical sign
- tells you to get the nth root
square root = v
cube root = 3v
- it is removed after you get the nth root
3. index
- tells to what root you should extract
When
converting radicals into exponents, the exponent of the radicand
becomes the numerator of the fraction, and the root of the radical
becomes the denominator of the fraction.
Examples:
1. 3v52
Answer: 5 2/3
2 – exponent; 3 – index = 2/3
2. 3v10
Answer: 10 1/3
1 – exponent; 3 – index = 1/3
3. v8
Answer: 8 ½
1- exponent; 2 – index = 1/2
4. 3v22
Answer: 22 1/3
1 – exponent; 3 – index = 1/3
5. v122
Answer: 12
2 – exponent; 2 – index = 2/2
The
quotient or ratio of two polynomials is called a rational expression.
Rational expressions are to polynomials what rational numbers are to
integers. A rational expression is nothing more than a fraction in
which the numerator and/or the denominator are polynomials. Here are
some examples of rational expressions:
![]()
The last one may look a little strange since it is more commonly written ![]()
![]() .
However, it’s important to note that polynomials can be thought of as
rational expressions if we need to, although they rarely are.
.
However, it’s important to note that polynomials can be thought of as
rational expressions if we need to, although they rarely are.
There
is an unspoken rule when dealing with rational expressions that we now
need to address. When dealing with numbers we know that division
by zero is not allowed. Well, the same is true for rational
expressions. So, when dealing with rational expressions we will
always assume that whatever x is it won’t give division by zero. We rarely write these restrictions down, but we will always need to keep them in mind.
For the first one listed we need to avoid x=1.
The second rational expression is never zero in the denominator and so
we don’t need to worry about any restrictions. Note as well that
the numerator of the second rational expression will be zero.
That is okay, we just need to avoid division by zero. For the
third rational expression we will need to avoid m=3 and m=-2.
The final rational expression listed above will never be zero in the
denominator so again we don’t need to have any restrictions.
Excluded Values:
Whenever
an expression containing variables is present in the denominator of a
fraction, you should be alert to the possibility that certain values of
the variables might make the denominator equal to zero, which is
forbidden. This means that when we are talking about rational
expressions we can no longer say that the variable represents “any real
number.” Certain values may have to be excluded. For example, in the
expression
![]() , we cannot allow the value x = 0 so we would parenthetically add the comment (x ¹ 0),
, we cannot allow the value x = 0 so we would parenthetically add the comment (x ¹ 0),
and for
![]() we would say (x ¹ 3) .
we would say (x ¹ 3) .
It
is important to keep this in mind as you work with rational
expressions, because it can happen that you are trying to solve an
equation and you get one of the “forbidden” values as a solution. You would have to discard that solution as being unacceptable. You can also get some crazy results if you don’t pay attention to the possibility that the denominator might be zero for certain values of the variable. For example, the celebrated proof that 0 = 1 and other nonsense. For example:
Let x = 1. Then
| Given: | x = 1 |
| Multiply both sides by x: | x2 = x |
| Subtract x from both sides: | x2 – x = 0 |
| Factor out an x: | x(x – 1) = 0 |
| Divide both sides by (x - 1): | x = 0 |
| But x = 1, so substitute 1 for x to get: | 1 = 0 |
This is wrong because we are dividing by zero because if x = 1 then (x – 1) = 0. Thus, all of these “proofs” are invalid because they use an illegal step.
What is a Rational Expression?
A rational expression is an algebraic expression of the form P/Q, where P and Q are simpler expressions (usually polynomials), and the denominator Q is not zero.
Examples:
| (a) | 1 | | P = 1, Q = x - 1 |
| (b) | 2xy - y2 | | P = 2xy - y2, Q = 2x2 - 1 |
A
“rational expression” is a polynomial fraction and anything you could
do with regular fractions, you could do with rational expressions.
However, since there are variables in rational expressions, there are
some additional considerations.
When
you dealt with fractions, you knew that the fraction could have any
whole numbers for the numerator and denominator, as long as you didn't
try to divide by zero. When dealing with rational expressions, you will
often need to evaluate the expression, and it can be useful to know
which values would cause division by zero, so you can avoid these x-values. So probably the first thing you'll do with rational expressions is find their domains.
The domain is all values that x is allowed to be. Since I can't divide by zero (division by zero isn't allowed), I need to find all values of x that would cause division by zero. Then the domain will be all other x-values. And when is the denominator equal to zero? When x = 0.
Then the domain is "all x not equal to zero".
The
domain doesn't care what is in the numerator of a rational expression.
The domain is only influenced by the zeroes of the denominator. Will
"3" ever equal zero? Of course not. Since the denominator will never
equal zero, no matter what value x is, then there are no forbidden values, and x can be anything. So the domain is "all x".
Exponential Laws Enter expressions that match the standard form shown on the right of each law. | |
| power of a power law: | xmxn = xm+n (xy)m = xm ym (xm)n =xmn xm ??xn = xm-n (x/y)m = xm / ym = xmy-m 1/x-m = xm a(x+c) = ax +ac |
| Power Property | Example | General Rule |
| addition | 32 + 34 = 32 + 34 = 9 + 81 = 90 | xm + xn = xm + xn Use BEDMAS to solve. |
| subtraction | 32 - 34 = 32 - 34 = 9 - 81 = -72 | xm - xn = xm - xn Use BEDMAS to solve. |
| product law | 3334 = (3x3x3) (3x3x3x3) = 33+4 = 37 | xmxn = xm+n Keep the common base, then add the exponents. |
| x2x6 = (xx) (xxxxxx) = x2+6 = x8 | ||
| power of a power law | (22)3 = (2x2)(2x2)(2x2) = 22x3 =26 | (xm)n = xmn Keep the base, then multiply the exponents. |
| (x3)4 = (xxx)(xxx)(xxx)(xxx) = x3x4 =312 | ||
| power of a product law | (3b)3 = (3b)(3b)(3b) = (3x3x3)(bbb) = 33b3 or (3b)3 = (31b1)3 = 31x3b1x3 = 33b3 | (xy)m = xm ym |
| (xy)4 = (xy)(xy)(xy)(xy) = (xxxx)(yyyy) = x4y4 or (xy)4 = (x1y1)4 = x1x4y1x4 = x4y4 | ||
| quotient law | 35 ??32 = (3x3x3x3x3)/(3x3) = 35-2 = 33 | xm ??xn = xm-n Keep the common base, then subtract the exponents. |
| x6 ??x2 = (xxxxxx)/(xx) = x6-2 = x4 | ||
| power of a quotient law | (3/b)3 = (3/b)(3/b) (3/b) = (3x3x3) /(bbb) = 27/b3 or (3/b)3 = (31b1)3 = 31x3/b1x3) = 33/b3 = 27/b3 | (x/y)m = xm ??ym |
| (x/y)4 =(x/y) (x/y) (x/y) (x/y) = (xxxx) /(yyyy) = x4/y4 or (x/y)4 = (x1/y1)4 = x1x4/y1x4 = x4/y4 | ||
| negative exponents | 3-4 = (1/3)4 = 1/34 | x-m = (1/x)m = 1/xm |
| x-3 = (1/x)3 = 1/x3 | ||
| 1/y-4 = (y/1)4 = y4 | 1/x-m = x |
A. We will define expressions so that the rules for exponents shall apply to these rational exponents.
Suppose that x = (51/3)3
x = 51/3 · 3
x = 51 or 5
Since x3 = 5, then x is the number whose cube is 5 or x3v5. Notice that we also know that x = 51/3, this means that 51/3 is equal to 3v5.
Reminder:
If n is a positive integer greater than 1 and ![]() is a real number, then a1/n =
is a real number, then a1/n = ![]() .
.
The denominator of the rational exponent corresponds to the index of the radical.
Examples:
41/2 = v4 = 2
-91/2 =- v9 = -3
5y1/3 = 53vy
B. Let us now expand our use of exponents to include m/n. We define their menaing so that rules for exponents still hold true. For example, by the properties of exponents.
Reminder:
If m and n are positive integers greater than 1 with m/n in lowest terms, then
Am/n = nvam = (nva)m
Examples:
82/3 = (81/3)2 = (3v8)2 or 82/3 = (82)1/3 = 3v82
C.
The rational exponents we have given meaning to exclude negative
rational numbers. To completes the set of definitions, we define a.
Reminder:
a –m/n = 1/am/n = 1 as long as am/n is a non-zero real number.
A. Square root of a number m is a number n such that n2 = m.
25 has a square root of 5 because 52 = 25.
25 also has a square root of -5 because (-5)2 = 25
-16 does not have a square root because there is no real number n2 = -16
Reminder:
Every positive real number has 2 real-number square roots.
The number 0 has just one square root, 0 itself.
Negative numbers do not have real-number square roots.
Examples:
v9 = 3
v36 = 6
v64 = -8
The principal root of a non-negative number is its non-negative square root. The symbol va represents the principal square root of a. The negative square too of a is written as -va.
B. The cube root of a number m3 is n real number has exactly on cube root in the system of real numbers. The symbol 3va represents the cube root of a.
Examples:
3v8 = 2
3v7 = 3
3v-8 = -2
Definition of the Nth Root:
In an = b, where a and b are real numbers and n is a positive integer, a is an nth root of b. It can also be written as nvb = a.
The nth root is the number that must be multiplied to itself n times to reach a given value.
Examples of Nth Root:
The following are some examples of nth root.
1) 3 is the 4th root of 81. That is, 3 has to be multiplied by itself 4 times to give 81.
2) 2 is the 6th root of 64. That us, 2 has to be multiplied by itself 4 times to give 64.
3) 4 is the square root of 16.
4) 5 is the cube root of 125.
TRY THIS:
Find 6v64a6b12
Choices:
a. 2ab2
b. 2a2b2
c. 2a6b2
d. 2a2b
CORRECT ANSWER: A
Step 1: 6v64a6b12
Step 2: = 6v(2)6 a6 (b2)6
Step 3: = 6v(2ab2)6
Step 4: = 2ab2
If n is odd, then ![]() is always a real number.
is always a real number.
For example, 3v8 and 3v-8 are both real numbers because 3v8 = 2 and 3v-8 = -2.
If n is even, then ![]() is a real number only when a < 0.
is a real number only when a < 0.
For example, v25 = 5 but v-25 is not a real number because 5 · 5 ? -25 and (-5) · (-5) ? -25.
| n | nth root | symbol |
| 2 | square root | v |
| 3 | cube root | 3v |
| 4 | fourth root | 4v |
| 5 | fifth root | 5v |
Example:
1) Find 4v625.
a. find the prime factorization of 625
625 = 5 · 5 · 5 · 5 = 54.
b. since 54 = 625 and 5 is positive, 4v625 = 5